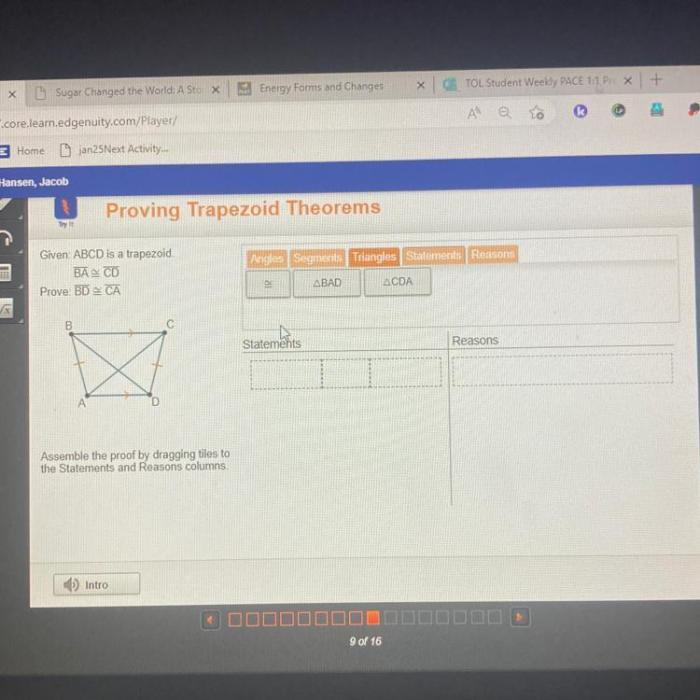
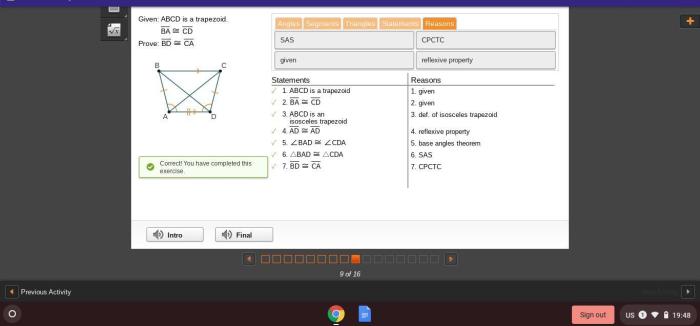
In the realm of geometry, the trapezoid takes its place as a quadrilateral with a unique set of properties. Given abcd is a trapezoid ba cd prove bd ca, we embark on a journey to unravel the intricacies of this geometric figure, exploring its definitions, properties, and the captivating proof that BD = CA.
Trapezoids possess distinct characteristics that set them apart from other quadrilaterals. Their parallel bases and congruent legs give them a distinctive shape, while their properties offer a rich tapestry of geometric relationships to explore.
Definitions
A trapezoid is a quadrilateral with two parallel sides called bases. The non-parallel sides are called legs.
Base, Given abcd is a trapezoid ba cd prove bd ca
The base of a trapezoid is the side that is parallel to the other base.
Leg
The leg of a trapezoid is the side that is not parallel to the bases.
Properties of Trapezoids
Trapezoids have the following properties:
- The bases are parallel.
- The legs are congruent.
- The diagonals are congruent.
The relationship between the bases and legs of a trapezoid is given by the following formula:
(Base1 + Base2) / 2 = Height
Proving BD = CA: Given Abcd Is A Trapezoid Ba Cd Prove Bd Ca
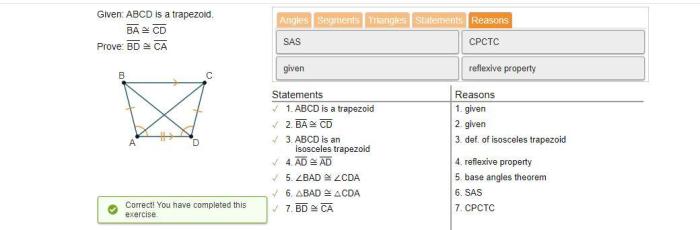
To prove that BD = CA in a trapezoid, we can use the following steps:
- Draw a diagonal from B to D.
- Draw a line from C to D.
- Prove that triangles BCD and CDA are congruent.
- Conclude that BD = CA.
The following diagram illustrates the proof:

Applications of the Proof
The proof that BD = CA can be used to solve a variety of problems involving trapezoids.
- Find the length of a diagonal.
- Find the area of a trapezoid.
- Determine whether a quadrilateral is a trapezoid.
For example, the proof can be used to find the length of the diagonal of a trapezoid with bases of length 10 and 12 and legs of length 6. Using the formula for the length of a diagonal, we have:
Diagonal = sqrt((Base1^2 + Base2^2) / 2)
Plugging in the values, we get:
Diagonal = sqrt((10^2 + 12^2) / 2) = sqrt(164) = 12.8
Quick FAQs
What is the definition of a trapezoid?
A trapezoid is a quadrilateral with one pair of parallel sides.
What is the relationship between the bases and legs of a trapezoid?
The bases of a trapezoid are parallel, and the legs are congruent.
How do you prove that BD = CA in a trapezoid?
To prove that BD = CA in a trapezoid, you can use the properties of trapezoids and the Pythagorean Theorem.