The length of a rectangle is 9.7 cm more than – The relationship between the length and width of a rectangle is a fundamental concept in geometry. Understanding this relationship is crucial for various applications, ranging from construction to design. This exploration delves into the intricacies of this relationship, examining how it impacts the perimeter and area of a rectangle, and uncovering its significance in real-world scenarios.
The concept of length difference, the disparity between the length and width of a rectangle, plays a significant role in determining the rectangle’s overall dimensions and proportions. By exploring the methods to calculate this difference and its impact on the rectangle’s properties, we gain a deeper understanding of how these dimensions interact.
Length and Width Relationship
A rectangle is a two-dimensional shape with four right angles. The length of a rectangle is the distance between the two longest sides, while the width is the distance between the two shorter sides. The relationship between the length and width of a rectangle is expressed by the formula:
L = W + d
where L is the length, W is the width, and d is the length difference.
For example, a rectangle with a length of 10 cm and a width of 6 cm has a length difference of 4 cm.
Calculating Length Difference: The Length Of A Rectangle Is 9.7 Cm More Than

To calculate the length difference of a rectangle, follow these steps:
- Subtract the width from the length: L
W = d
- The result is the length difference.
For example, to find the length difference of a rectangle with a length of 12 cm and a width of 8 cm, we subtract 8 cm from 12 cm:
12 cm
8 cm = 4 cm
Therefore, the length difference is 4 cm.
Perimeter and Area Impact
The length difference of a rectangle affects its perimeter and area.
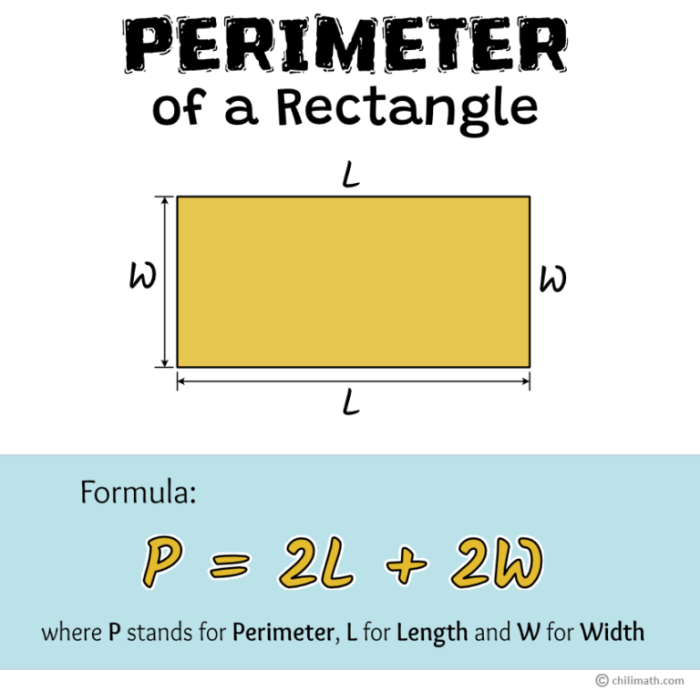
The perimeter of a rectangle is the sum of all four sides. The formula for the perimeter is:
P = 2L + 2W
where P is the perimeter, L is the length, and W is the width.
The area of a rectangle is the product of the length and width. The formula for the area is:
A = L x W
where A is the area, L is the length, and W is the width.
As the length difference increases, the perimeter and area of the rectangle will also increase.
Real-World Applications
Understanding the length difference of a rectangle is important in many real-world applications, such as:
- Construction:When building a house or other structure, it is important to ensure that the dimensions of the walls and other components are correct. The length difference between the walls can affect the overall stability of the structure.
- Design:When designing a product or a space, it is important to consider the length difference of the different components. This can affect the aesthetics and functionality of the design.
- Engineering:When designing a machine or other mechanical device, it is important to consider the length difference between the different components. This can affect the efficiency and performance of the device.
Q&A
What is the formula for calculating the length difference of a rectangle?
Length difference = Length – Width
How does length difference affect the perimeter of a rectangle?
Length difference directly influences the perimeter of a rectangle. A greater length difference results in a larger perimeter.
Can you provide an example of a real-world application of length difference?
In architecture, understanding length difference is crucial for designing rectangular rooms with specific dimensions and proportions.