Write a quadratic function f whose zeros are and – In the realm of mathematics, quadratic functions hold a prominent position, providing a powerful tool for modeling various real-world phenomena. Understanding the construction of quadratic functions given their zeros is crucial for harnessing their full potential.
This comprehensive guide delves into the intricacies of quadratic functions, exploring methods for determining their zeros and techniques for constructing functions with specified zeros. By delving into the fundamental concepts and practical applications of quadratic functions, we embark on a journey of mathematical discovery.
1. Overview of Quadratic Functions

Quadratic functions are functions that can be expressed in the general form f(x) = ax2+ bx + c , where a, b, and care real numbers and ais not equal to 0. The graph of a quadratic function is a parabola.
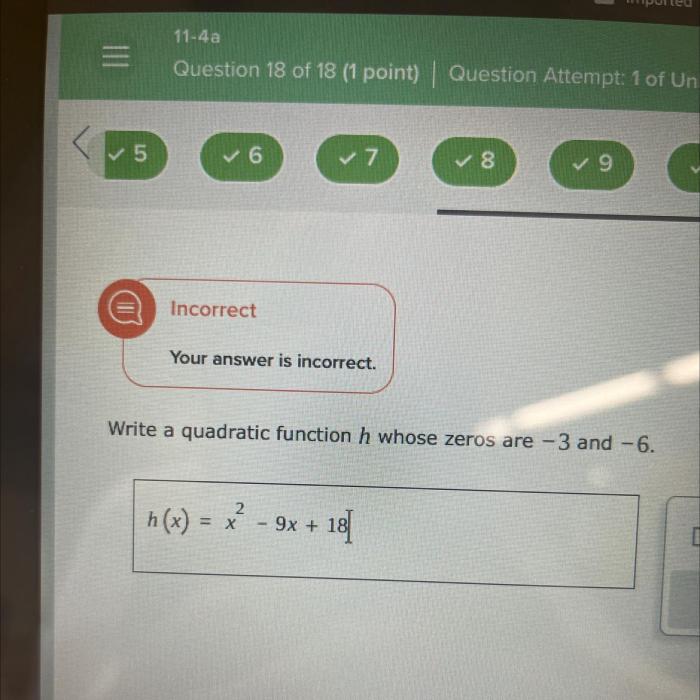
The zeros of a quadratic function are the values of xfor which f(x) = 0. The zeros of a quadratic function can be found by factoring, using the quadratic formula, or completing the square.
2. Determining Zeros of a Quadratic Function
Factoring
If a quadratic function can be factored into the form f(x) = (x- r 1)(x – r 2) , then the zeros of the function are r1and r2.
Quadratic Formula
The quadratic formula can be used to find the zeros of any quadratic function. The quadratic formula is:
x = (-b ± √(b2
4ac)) / 2a
Completing the Square, Write a quadratic function f whose zeros are and
Completing the square can be used to find the zeros of any quadratic function. Completing the square involves adding and subtracting the square of half the coefficient of xto the function.
3. Constructing Quadratic Functions with Given Zeros
To construct a quadratic function with given zeros r1and r2, use the following steps:
- Write the function in factored form: f(x) = (x
- r1)(x
- r 2)
- Expand the function: f(x) = x2
(r1+ r 2)x + r 1r 2
The resulting function will have zeros r1and r2.
4. Applications of Quadratic Functions
Quadratic functions are used in a variety of applications, including:
- Modeling projectile motion
- Optimizing shapes
- Solving problems in physics, engineering, and economics
5. Advanced Concepts
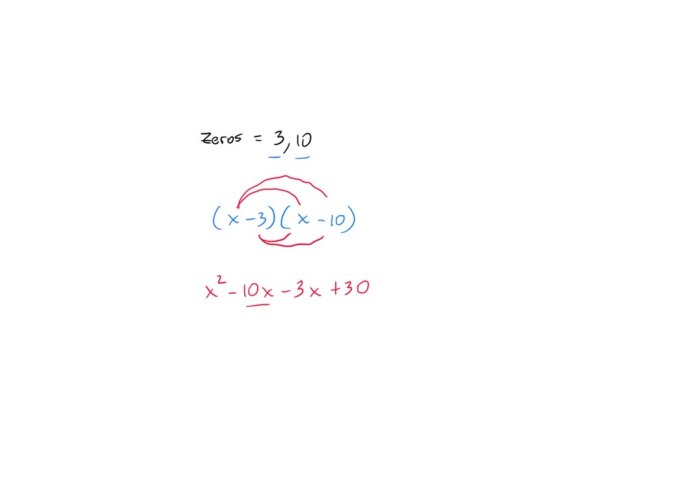
Vertex Form
The vertex form of a quadratic function is f(x) = a(x- h) 2+ k , where (h, k)is the vertex of the parabola.
Discriminant
The discriminant of a quadratic function is the expression b2– 4ac . The discriminant determines the number and nature of the zeros of the function.
FAQ: Write A Quadratic Function F Whose Zeros Are And
What is the discriminant of a quadratic function?
The discriminant is a term that appears in the quadratic formula and determines the nature of the roots of the quadratic function. It is calculated as b^2 – 4ac, where a, b, and c are the coefficients of the quadratic function.
How can I determine the zeros of a quadratic function?
There are several methods to find the zeros of a quadratic function, including factoring, using the quadratic formula, or completing the square.
What are some real-world applications of quadratic functions?
Quadratic functions have numerous applications in various fields, such as modeling projectile motion, optimizing shapes, and solving problems in physics, engineering, and economics.